每日算法

计划寒假期间至少保证每天一道新题，随时复习之前未AC的旧题

标*的题目是第一次没有AC，看了答案的，后面需要多次巩固

博客灵感来源：LeetCode每日一题（新） | HillZhang的博客 (gitee.io)

2024.1

9. 回文数（Easy）

题目描述

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。例如，121 是回文，而 123 不是。

示例 1：

1
2
输入：x = 121
输出：true

示例 2：

1
2
3
输入：x = -121
输出：false
解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

题解

法1：双指针法

非常蠢笨易想的一种方法，看到这道题脑子第一反应就是这个，同时考虑到负数不可能是回文数，所以直接对所有负数返回false；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int len(int x) {
        int length = 0;
        while (x != 0) {
            length++;
            x /= 10;
        }
        return length-1;
    }

    bool isPalindrome(int x) {
        int front, end, i = 0, j = len(x);
        if (x < 0)
            return false;
        if (x == 0)
            return true;
        string a = to_string(x);
        while (i != j && i < j) {
            if (a[i] != a[j])
                return false;
            else {
                i++;
                j--;
            }
        }
        return true;
    }
};

法2：反转一半数字

将数字本身反转，将反转后的数字和原始数字进行比较，若相同则该数字回文，同时为避免数字反转可能导致的溢出问题，只考虑反转int的一半（毕竟回文数后半段反转后应该与前半段相同）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool isPalindrome(int x) {
        if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }
        int revertedNumber = 0;
        while (x > revertedNumber) {
            revertedNumber = revertedNumber * 10 + x % 10;
            x /= 10;
        }
        return x == revertedNumber || x == revertedNumber / 10;
    }
};

2024.3

不要问为什么隔了这么久……

142.环形列表②（Medium）

题目描述

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

img

1
2
3
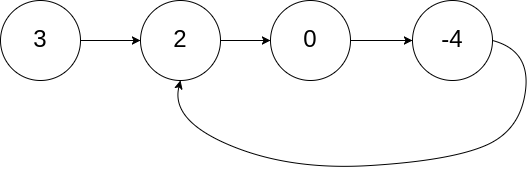
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

题解

对于链表找环路问题，有一个通用的解法——Floyd判圈法

Floyd判圈法

快指针和慢指针以1:2的速度前进。
当快指针再次与慢指针相遇时，它们行进路程的差值一定为圈长的整数倍。
设进入圈前的链长为m，圈长为L，慢指针走了a圈，快指针走了b圈，它们第一次相遇在距离入圈点d的位置，则

$$S = m + a*L + d $$

$$2S = m + b*L + d$$

解得 $m = (a-2b)*L-d$
考虑模拟上述过程，在两个指针再次相遇时停下来。
此时将慢指针移动至初始结点，快指针不动，以$1:1$的速度继续前进。
思考一下，由于两指针此时速度相同，若是能相遇，则相遇点只能为入圈点，那么根据行进路程可得以下等式

$$m = n*L - d$$

将m代入得 $(a-2b)L = nL$ 一定成立。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast = head;
        ListNode *slow = head;
        do {
            if (fast == NULL || fast->next == NULL) return NULL;
            fast = fast->next->next;
            slow = slow->next;
            // if (fast == NULL) return NULL;
        } while (fast != slow);
        slow = head;
        while (fast != slow) {
            slow = slow->next;
            fast = fast->next;
        }
        return fast;
    }
};

76.最小覆盖子串（Hard）

题目描述

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。
1
2
3
输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

进阶要求：时间复杂度不超过$O(n)$

题解

本题使用滑动窗口求解，两个指针均从左向右移动，且l永远在r的左边或重合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    string minWindow(string s, string t) {
        vector<int> chars(128,0);
        vector<bool> flag(128,false);
        //统计t字符串数据
        for (int i=0;i<t.size();i++) {
            flag[t[i]] = true;
            ++chars[t[i]];
        }
        //开始滑动窗口了
        int count = 0,l=0,min_l=0,min_size=s.size()+1;
        for (int r=0;r<s.size();r++) {
            if(flag[s[r]]) {
                //还缺这个字符
                if (--chars[s[r]] >= 0) {
                    count++;
                }
                //已经包含所有字符，尝试将l右移
                while (count == t.size()) {
                    //更新
                    if (r - l + 1 < min_size) {
                        min_size = r - l + 1;
                        min_l = l;
                    }
                    //右移窗口
                    if(flag[s[l]] && ++chars[s[l]]>0) {
                        --count;
                    }
                    l++;
                }
            }
        } 
        return min_size>s.size()? "" :s.substr(min_l,min_size);
    }
};

一点++和–的小技巧：

a++和++a均是将a+1，但a++返回值为a，++a的返回值为a+1.如果只是希望增加a的值，而不需要返回值，推荐使用++a，运行速度略快一些。

633. 平方数之和（Medium）

题目描述

给定一个非负整数 c ，你要判断是否存在两个整数 a 和 b，使得

$$ a^2 + b^2 = c $$

1
2
3
输入：c = 5
输出：true
解释：1 * 1 + 2 * 2 = 5

题解

法1：暴力遍历

这道题其实非常基础，无非是使用双指针前后移动寻找合适的解，主要问题在于如何降低时间复杂度。根据题目可以知道c的取值最大为2^31。若是l指针从左至右，r指针从右至左，不难想到溢出问题。既然是求平方和，a和b的大小不可能大于c的平方，因此r指针可以从根号c开始遍历。考虑一下极端情况，例如c的值为2147482647时，平方和相加一旦大于c，int就会溢出，所以可以将指针和sum的数据类型定义为long。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    bool judgeSquareSum(int c) {
        if (c == 0 || c == 1) return true;
        long l = 0,r = sqrt(c);
        long sum;
        while (l<=r) {
            sum = l*l + r*r;
            if(sum == c) return true;
            if(sum < c) ++l;
            else if(sum > c) --r;
        }
        return false;
    }
};

法2：数学思维

根据前几个数 1 = 0 + 1；4 = 1 + 3； 9 = 4 +5；16 = 9+7;

不难看出，所有平方数都可以化作一个奇数与前一个平方数的和。因此可以将c每次减少一个奇数，判断剩下的数是否为平方数。由于等差数列

$$ 1 + 3 + 5 + 7 +… +2n-1 = n^2 $$

减去的数之和也为平方数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool judgeSquareSum(int c) {
       int num = sqrt(c);
       if ( num*num == c ) return true;
       for (int i = 1;i<c;i+=2) {
           c -= i;
           if (c<0) break;
           num = sqrt(c);
           if (num*num == c) return true;           
       }
       return false;
    }
};

680.验证回文串②（Easy）

题目描述

给你一个字符串 s，最多 可以从中删除一个字符。

请你判断 s 是否能成为回文字符串：如果能，返回 true ；否则，返回 false 。

1
2
输入：s = "aba"
输出：true

题解

利用双指针从两头遍历字符串，判断是否是回文串，若不是回文串，则尝试删除一个字符（即查看下一个字符是否与另一边相同），由于只能删除一个，所以添加一个flag属性标记是否有过修改……思路没毛病，但似乎忽略了一些东西。

根据上面的内容写出代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool validPalindrome(string s) {
        int l = 0,r = s.length()-1;
        bool flag = false;
        while(l<=r) {
            if (s[l]!=s[r]) {
                if (flag) return false;
                else {                    
                    if (s[r-1] == s[l]) --r;
                    else if (s[l+1] == s[r]) ++l;
                    else return false;
                    flag = true;
                }
            }
            ++l;--r;
        }
        return true;
    }
};

很显然，上述代码先查看右边的行不行再看左边的，仅仅检验了一位，删除后会继续遍历，这样得出的结果仅是局部最优解，很容易就被套路住了（

例如第460多个测试用例"lcupuufxooxfuupucul" "bececabbacecb”

因此，我们无法通过仅判断相邻字符确定删除哪一边的字符，就只好将两种删除情况分别遍历，最后取或运算即可。所幸只能删除一个元素，最多只需要遍历两个字符串，并不会增加太多负担。修改后代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool validPalindrome(string s) {
        int l = 0,r = s.length()-1;
        while(l<=r) {
            if (s[l]!=s[r]) {
               return Palindrome(s,l+1,r) || Palindrome(s,l,r-1);                                  
            }
            ++l;--r;
        }
        return true;
    }
    bool Palindrome(string s,int l,int r) {
        while(l<=r) {
            if(s[l]!=s[r]) return false;
            ++l;--r;
        }
        return true;
    }
};

524.通过删除字母匹配到字符串（Medium）

题目描述

给你一个字符串 s 和一个字符串数组 dictionary ，找出并返回 dictionary 中最长的字符串，该字符串可以通过删除 s 中的某些字符得到。

如果答案不止一个，返回长度最长且字母序最小的字符串。如果答案不存在，则返回空字符串。

1
2
输入：s = "abpcplea", dictionary = ["ale","apple","monkey","plea"]
输出："apple"

题解

首先分析题目，我们需要确定dictionary数组中的字符串是否为s的子串，这个验证可以采用双指针进行匹配，定义两个指针m和n，分别指向s和dictionary中某一个字符串的首位字符，m指针依次向右遍历s字符串，若遇到相同字符，则n指针向右移动。直至到达字符串尾。此时若目标子串遍历完成，即确定它是s的子串，则需要考虑是否为最优解。通过定义max_s属性记录当前最优解。由于题目要求返回长度最长且字母序最小的字符串，则可以在进入双指针匹配前就将长度短于目前最优解的字符串排除。因此只需考虑更长的和长度相等但字母序不同的字符串。

长度更长，毫无疑问是更优解，需要更新max_s；若长度相等但字母序更小，也需要更新max_s。最后将max_s返回即可。

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    string findLongestWord(string s, vector<string>& dictionary) {
        string max_s = "";
        for (int i=0;i<dictionary.size();i++) {
            if (dictionary[i].length() < max_s.length()) continue;
            int m = 0,n = 0;
            while (m <= s.length() && n <= dictionary[i].length()) {
                if (s[m] == dictionary[i][n]) ++n;
                ++m;
                if(n > dictionary[i].length()) {
                    if (dictionary[i].length() > max_s.length() || (dictionary[i].length() == max_s.length() && dictionary[i] < max_s))
                    max_s = dictionary[i];    
                }            
            }
        }
        return max_s;
    }
};

2024.4

69. x的平方根（Easy）

题目描述

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

1
2
3
输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

题解

起初：这不轻轻松松简简单单

程序：超时超时超时

由于题目限制x为非负整数，我们可以知道在[0,x]区间内一定能找到一个符合要求的算术平方根。将0的情况单独考虑，在区间[1,x]内进行二分查找，使用闭区间的写法即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int mySqrt(int x) {
        if (x==0) return 0;
        int l = 1,r = x;
        int half,sqr;
        while (l <= r) {
            half = l + (r-l)/2;
            sqr = x/half;
            if (half == sqr) return half;
            if (sqr > half) l = half+1;
            else if (sqr < half) r = half-1;
        }
        return r;
    }
};

法2：牛顿迭代法

公式为

$$ x_{n+1} = x_n - f(x_n)/f’(x_n)$$

其中给定

$$ f(x) = x^2 - a = 0 $$

可算出迭代公式为

$$ x_{n+1} = (x_n + a/x_n)/2 $$

1
2
3
4
5
6
7
8
9
10
class Solution {
		public:
			int mySqrt(int x) {
				long a = x;
				while (a*a > x) {				
					a = (a + x/a) / 2;
				}
				return a;				
			}
}

34.在排序数组中查找元素的第一个和最后一个位置（Medium）

题目描述

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 ：

1
2
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

题解

最直接的思路肯定是使用双指针从前往后遍历一便，找到目标元素第一次和最后一次出现的坐标，但这样的时间复杂度为O(n) ，不符合题目的要求，且没有用到有序数组的条件。

由于题目要求时间复杂度为 O(log n) ，此题需使用二分查找的方法，加上是有序数组，可以轻易地拥有查找思路，但是该怎么准确地分辨出起始和终止的位置呢。最终代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {     
        if(nums.empty()) return vector<int>{-1,-1};
        int begin = searchleftRange(nums,target);
        int end = searchRightRange(nums,target);
        
        if ( begin == nums.size() || nums[begin] != target) {
            return vector<int>{-1,-1};
        }
        return vector<int>{begin,end};
    }
    
    int searchleftRange(vector<int>& nums, int target) {        
        int l = 0,r = nums.size();   
        while(l < r) {            
            int mid = (r+l)/2;
            if (nums[mid] >= target) r = mid;            
            else if (nums[mid] < target) l = mid+1;
        }
        
        return r;
        
    }
    
    int searchRightRange(vector<int>& nums, int target) {        
        int l = 0,r = nums.size();   
        while(l < r) {            
            int mid = (r+l)/2;
            
            if(nums[mid] == target && (mid+1 >= nums.size() || nums[mid+1] > target)) 
                    return mid; 
            if (nums[mid] <= target) l = mid+1;            
            else if (nums[mid] > target) r = mid-1;
        }
        
        return r;
        
    }
};

由于对区间知识的不熟悉，很明显这是一种有点混乱的写法（

看到了一个思路，左侧查找第一个等于target的值，右侧查找值为第一个大于target的位置-1，这样的话显然比上面那个合理多了（，只需要修改searchRightRange函数，以及end的赋值，改后如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {     
        if(nums.empty()) return vector<int>{-1,-1};
        int begin = searchleftRange(nums,target);
        int end = searchRightRange(nums,target)-1; // 首个大于target的索引-1
        
        if ( begin == nums.size() || nums[begin] != target) {
            return vector<int>{-1,-1};
        }
        return vector<int>{begin,end};
    }
    
    int searchleftRange(vector<int>& nums, int target) {    
	    //……    
    }
    int searchRightRange(vector<int>& nums, int target) {        
        int l = 0,r = nums.size();   
        while(l < r) {            
            int mid = (r+l)/2;           
            if (nums[mid] <= target) l = mid+1;            
            else if (nums[mid] > target) r = mid;
        }
        
        return r;
        
    }
};

81.搜索旋转排序数组②（Medium）

题目描述

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

你必须尽可能减少整个操作步骤。

来点讨厌的示例

1
2
3
4
5
6
输入：[1,1,1,1,1,1,1,1,1,13,1,1,1,1,1,1,1,1,1,1,1,1] 13
输出：true
输入：[1,0,1,1,1] 0
输出：true
输入：[1,3,5] 5
输出：true

题解

由于本人正在做二分查找的系列题，所以这道题毫不犹豫进行二分。由于是一个旋转后的数组，是部分顺序排列的，所以可以通过和区间起始点或结束点的比较来判断这部分是否为有序，否则另一部分有序。为了方便，我们可以先进入有序区间进行查找，若该区间没有目标值，则继续二分查找另一区间。

同时，由于每个数字并不唯一，可能出现无法判断是否有序的情况，例如若起始点与区间中点的值相同，则无法断言左区间是否有序，此时可将起始点+1，继续查找新区间的中点，直到可以判断是否有序为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    bool search(vector<int>& nums, int target) {
         int l = 0,r = nums.size()-1;
         int mid;
         while (l <= r) {
            mid = l + (r-l)/2;
            if(nums[mid] == target) return true;

            if (nums[l] == nums[mid]) ++l; 
            else if (nums[mid] > nums[l]) {  //左端已排好序            
                if (nums[l] == target) return true;
                else if (nums[l] > target || nums[mid] < target) //不存在target
                    l = mid+1;                    
                else
                    r = mid-1;               
            } else 
                if (nums[r] == target) return true;
                else if (nums[r] < target || nums[mid] > target) 
                    r = mid-1;
                else  
                    l = mid+1;            
         }
         return false;
    }
};

153.寻找数组最小值（Medium）

题目描述

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组

1
nums = [0,1,2,4,5,6,7]
  • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
  • 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

题解

根据旋转的定义，我们可以判断出，在旋转后的数组中，最小值左侧数组是有序的，最小值右侧也是有序的，并且右侧的值恒比左侧小。在二分查找时，我们可以将数据大小进行比较。若区间右侧nums[r]大于区间中点nums[mid] ，则可以确定最小值min不可能出现在mid右侧，下一次查找不必考虑右侧的数据；若区间右侧nums[r] 小于区间中点nums[mid] ，则最小值min出现在mid右侧，此时不必考虑左侧的数据，以此查找，直到只剩一个数为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int findMin(vector<int>& nums) {
        int l = 0,r = nums.size()-1,mid;
        
        while (l <= r) {
            mid = l+(r-l)/2;
            
            if (nums[mid] < nums[r]) {
                r = mid;
            } else l = mid+1;            
        }        
        return nums[r];
    }
};

154.寻找旋转排序数组的最小值②（Hard）

题目描述

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，，得到输入数组。例如，原数组

1
nums = [0,1,4,4,5,6,7]

在变化后可能得到：

  • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
  • 若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个可能存在 重复 元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须尽可能减少整个过程的操作步骤。

题解

这道题是153题的进阶版，区别在于数组中含重复元素，整体思路大致相同，只需要多考虑重复的情况，由于重复元素并不会影响对于最小值的判断，此时可以将区间进行移动，剔除掉重复元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int findMin(vector<int>& nums) {
        int l = 0,r = nums.size()-1,mid;        
        while (l <= r) {
            mid = l+(r-l)/2;            
            if (nums[mid] == nums[r]) --r;            
            else if (nums[mid] < nums[r]) {
                r = mid;
            } else l = mid+1;            
        }        
        return nums[l];        
    }
};

单例模式 小明的购物车

事实证明这已经不再是一个只有leetcode的记录了……

题目描述

小明去了一家大型商场，拿到了一个购物车，并开始购物。请你设计一个购物车管理器，记录商品添加到购物车的信息（商品名称和购买数量），并在购买结束后打印出商品清单。（在整个购物过程中，小明只有一个购物车实例存在）。

输入包含若干行，每行包含两部分信息，分别是商品名称和购买数量。商品名称和购买数量之间用空格隔开。

输出包含小明购物车中的所有商品及其购买数量。每行输出一种商品的信息，格式为 “商品名称 购买数量”。

输入示例

1
2
3
Apple 3
Banana 2
Orange 5

输出示例

1
2
3
Apple 3
Banana 2
Orange 5

题解

简单起见，这里选用饿汉模式，即实例在类加载时就被创建，单例模式为了防止外部实例化，需要设置私有的构造方法，由于本题需要将商品名与数量同时存储且一一对应，故而选择Map进行存储。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import java.util.LinkedHashMap;
import java.util.Scanner;
import java.util.Map;


public class Main {
    public static void main(String[] args) {
        ShoppingCart cart = ShoppingCart.getInstance();
        
        Scanner sc = new Scanner(System.in);
        while(sc.hasNext()){
            String  itemName = sc.next();
            int number = sc.nextInt();
            
            cart.addToCart(itemName,number);
        }
        
        cart.viewCart();
    }
    
}

class ShoppingCart {
    private static final ShoppingCart instance = new ShoppingCart();
    
    private Map<String,Integer> cart;
    
    //私有构造方法
    private ShoppingCart() {
        cart = new LinkedHashMap<>();
    }
    
    //公开方法
    public void addToCart(String itemName,int number) {
        cart.put(itemName,number);
    }
    
    public void viewCart() {
        for  (Map.Entry<String, Integer> entry  : cart.entrySet()) {
            System.out.println(entry.getKey() + " " + entry.getValue());
        }    
        
    }
    
    public static ShoppingCart getInstance(){
        return instance;        
    }
}

*4.寻找两个正序数组的中位数（Hard）

题目描述

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 

1
2
3
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

题解

法1：寻找第k小

如果不考虑时间复杂度，这道题就简单得多了，比如说可以先将俩数组合并，取合并后数组的中位数，只可惜这样做的时间复杂度和空间复杂度均是O（m+n）。为了达到log级的复杂度，我们需要进行二分查找，此处一个十分巧妙的思路就是将寻找中位数转化为寻找第k小数，利用寻找第k小数的算法进行。

此处我们进行循环，每次循环排除前k/2个数字，即比较两个数组的第k/2个数字，排除掉较小的那部分，之后更新k值继续循环，此处k即为距离中位数还需要排除的数字个数。

此处有一种特殊情况，比如说两个数组[1],[2,3,4,5,6,7]，很明显第一个数组小于第二个数组，k=4，我们需要排除掉2个数字，但是第一个数组长度为1。为了防止越界，我们在排除前先比较k/2和当前数组的长度，取较小者进行排除。

若是排除后有一个数组为空了呢？为了减少比较次数，我们在每次递归的开始，便比较两个数组的长度，将较短的数组置于nums1的位置，这样即使有数组为空，我们也能肯定是第一个数组。此时仅需要在nums2中找到第k个位置返回即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(),n = nums2.size();
        int left = (m+n+1)/2;
        int right = (m+n+2)/2;
        return (findK(nums1,0,m-1,nums2,0,n-1,left)+findK(nums1,0,m-1,nums2,0,n-1,right))*0.5;
        
    }
    
    int findK(vector<int>& nums1,int start1,int end1,vector<int>& nums2,int start2,int end2,int k) {
        int len1 = end1 - start1 +1;
        int len2 = end2 - start2 +1;
        
        //确保len1是较短的那条
        if (len1 > len2) return findK(nums2,start2,end2,nums1,start1,end1,k);
        if (len1 == 0) return nums2[start2+k-1];
        
        if (k == 1) return min(nums1[start1],nums2[start2]);
        
        int i = start1 + min(len1,k/2) -1;
        int j = start2 + min(len2,k/2) -1;
        
        if (nums1[i] > nums2[j]) {
            return findK(nums1,start1,end1,nums2,j+1,end2,k-j+start2-1);
        } else {
            return findK(nums1,i+1,end1,nums2,start2,end2,k-i+start1-1);
        }

    }
};

法2：轮切（误）

时间复杂度更低，但水平不够没看明白，等弄明白了再补

工厂方法模式 积木工厂

题目描述

小明家有两个工厂，一个用于生产圆形积木，一个用于生产方形积木，请你帮他设计一个积木工厂系统，记录积木生产的信息。

输入描述

输入的第一行是一个整数 N（1 ≤ N ≤ 100），表示生产的次数。

接下来的 N 行，每行输入一个字符串和一个整数，字符串表示积木的类型。积木类型分为 “Circle” 和 “Square” 两种。整数表示该积木生产的数量

输出描述

对于每个积木，输出一行字符串表示该积木的信息。

输入示例

1
2
3
4
3
Circle 1
Square 2
Circle 1hell

输出示例

1
2
3
4
Circle Block
Square Block
Square Block
Circle Block

通过代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
import java.util.ArrayList;

import java.util.List;

import java.util.Scanner;

//抽象产品
interface Block {
    void block();
}

class Circle implements Block {
    @Override
    public void block() {
        System.out.println("Circle Block");
    }
}

class Square implements Block {
    @Override
    public void block() {
        System.out.println("Square Block");
    }
}

interface BlockFactory {
    Block createBlock();
}

class CircleFactory implements BlockFactory {
    @Override
    public Block createBlock() {
        return new Circle();
    }
}

class SquareFactory implements BlockFactory {
    @Override
    public Block createBlock() {
        return new Square();
    }
}

public class Main {
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        BlockFactory circleFactory = new CircleFactory();
        BlockFactory squareFactory = new SquareFactory();
        int N = sc.nextInt();
        for (int i=0;i<N;i++) {
            String shape = sc.next();
            int count = sc.nextInt();
            //System.out.println(shape.equals("Circle"));
            if(shape.equals("Circle")) {
                Block circle = circleFactory.createBlock();
                for(int j=0;j<count;j++){
                    circle.block();
                }   
            } else {
                Block square = squareFactory.createBlock();
                for(int j=0;j<count;j++){
                    square.block();
                }
            }
        }
        
    }
    
}

抽象工厂模式 家具工厂

题目描述

小明家新开了两个工厂用来生产家具，一个生产现代风格的沙发和椅子，一个生产古典风格的沙发和椅子，现在工厂收到了一笔订单，请你帮他设计一个系统，描述订单需要生产家具的信息。

输入描述

输入的第一行是一个整数 N（1 ≤ N ≤ 100），表示订单的数量。

接下来的 N 行，每行输入一个字符串，字符串表示家具的类型。家具类型分为 “modern” 和 “classical” 两种。

输出描述

对于每笔订单，输出字符串表示该订单需要生产家具的信息。

modern订单会输出下面两行字符串

modern chair

modern sofa

classical订单会输出下面两行字符串

classical chair

classical soft

输入示例

1
2
3
4
3
modern
classical
modern

输出示例

1
2
3
4
5
6
modern chair
modern sofa
classical chair
classical sofa
modern chair
modern sofa

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
import java.util.Scanner;

interface Sofa {
    void sofa();
}

interface Chair {
    void chair();
}

class ModernSofa implements Sofa {
    @Override
    public void sofa() {
        System.out.println("modern sofa");
    }
}

class ModernChair implements Chair {
    @Override
    public void chair() {
        System.out.println("modern chair");
    }
}

class ClassicalSofa implements Sofa {
    @Override
    public void sofa() {
        System.out.println("classical sofa");
    }
}

class ClassicalChair implements Chair {
    @Override
    public void chair() {
        System.out.println("classical chair");
    }
}

interface Factory {
    Sofa createSofa();
    Chair createChair();
}

class ModernFactory implements Factory {
    @Override
    public Sofa createSofa() {
        return new ModernSofa();
    }
    
    @Override
    public Chair createChair() {
        return new ModernChair();
    }
}

class ClassicalFactory implements Factory {
    @Override
    public Sofa createSofa() {
        return new ClassicalSofa();
    }
    
    @Override
    public Chair createChair() {
        return new ClassicalChair();
    }
}

public class Main {
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for(int i=0;i<n;i++) {
            String type = sc.next();
            Factory factory;
            if (type.equals("modern")) {
                factory = new ModernFactory();
            } else {
                factory = new ClassicalFactory();
            }
            Sofa sofa = factory.createSofa();
            Chair chair = factory.createChair();
            chair.chair();
            sofa.sofa();
        }   
    }   
}

2024.5

347. 前K个高频元素（Medium）

题目描述

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

1
2
输入：nums = [1,1,1,2,2,3],k = 2
输出：[1,2]

题解

由于需要统计单个元素的出现频率，可以采用桶排序来降低时间复杂度，首先需要遍历整个数组，统计所有元素及其出现频率，然后按照出现频率进行排列，选出最高的k位元素进行输出。由于数组中元素未知，采用字典较为合适，如map等，此处介绍一个基于哈希表实现的时间复杂度更低的数据类型

unordered_map

unordered_map和map类似，都是存储的key-value的值，可以通过key快速索引到value。不同的是unordered_map不会根据key的大小进行排序，存储时是根据key的hash值判断元素是否相同，即unordered_map内部元素是无序的。unordered_map的底层是一个防冗余的哈希表（开链法避免地址冲突）。unordered_map的key需要定义hash_value函数并且重载operator ==。

哈希表最大的优点，就是把数据的存储和查找消耗的时间大大降低，时间复杂度为O(1)；而代价仅仅是消耗比较多的内存。哈希表的查询时间虽然是O(1)，但是并不是unordered_map查询时间一定比map短，因为实际情况中还要考虑到数据量，而且unordered_map的hash函数的构造速度也没那么快，所以不能一概而论，应该具体情况具体分析。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
         unordered_map<int,int> counts;
         //记录出现的最高频数
         int max_count = 0;
         for (int & num : nums) {
             max_count = max(max_count,++counts[num]);
         }
         
         //桶
         vector<vector<int>> buckets(max_count+1);
         for (const auto & p : counts){
             buckets[p.second].push_back(p.first);
         }
         vector<int> ans;
         for (int i=max_count;i >= 0 && ans.size() < k; --i) {
             for(int & m : buckets[i]) {
                 ans.push_back(m);
                 if (ans.size() == k) break;
             }
         }
         
         return ans;
    }
};

215.数组中的第K个最大元素（Medium）

题目描述

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

题解

看到这个题目，很明显需要排序，该如何选择排序方式呢？我们可以选用内置的sort方法进行排序，然后返回数组的第nums.size()-k位即可，但是这个方法的时间复杂度为O(nlogn)，不符合题目中要求的O(n)。

题目要求返回第k大的数字即可，不需要将整个数组进行排序，根据快速排序原理，若某次划分后，基准数的索引刚好是n-k的话，意味着它就是我们要找的数字，此时可以直接将其返回，无需继续排列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int l = 0,r = nums.size()-1,target = nums.size()-k;
while(l<r) {
	      int mid = quick_selection(nums,l,r);
        if (mid == target) return nums[mid];
        else if (mid < target) l = mid+1;
        else r = mid-1;
    }
    return nums[l];
}

int quick_selection(vector<int>& nums,int l, int r) {
    int i = l+1,j = r;
    while(true) {
        while(i<r && nums[i] <= nums[l]) ++i;
        while(j>l && nums[j] >= nums[l]) --j;
        if (i >= j) break;

        swap(nums[i],nums[j]);
    }
    swap(nums[l],nums[j]);
    return j;
}
};

然而，若是考虑极端情况，若每次划分均将数组分为1和n-1，且第k大数每次都在n-1中，这种情况下快排的时间复杂度为O(N^2)。卡在了最后一个测试用例，在提交记录上看不完全，怀疑有特别长，最后超时

1
2
[2,3,4,5,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
5

观察这个用例不难发现，重复的元素特别多，而上述代码将重复元素等同于小于，所以会在上面做许多无用功，一种解决方案是使用三路划分，每轮将数组依照基准数划分为三个部分：小于、等于和大于。这样当发现第k大数处于等于基准数的子数组中时，可以直接返回该元素

为了提升算法的稳健型，这里采用随机选择的方式选定基准数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        return quick_selection(nums,k);
    }
    
    int quick_selection(vector<int>& nums,int k) {
        int pivot = nums[rand() % nums.size()];
        vector<int> big,equal,small;
        for(int i : nums) {
            if (i > pivot) 
                big.push_back(i);
            else if (i < pivot)
                small.push_back(i);
            else
                equal.push_back(i);
        }
        
        //第k大在big中
        if (k <= big.size()) 
            return quick_selection(big,k);
        //第k大在small中
        else if (k > big.size()+equal.size())
            return quick_selection(small,k-big.size()-equal.size());
        else
            return pivot;
    }
};

原型模式 矩形原型

题目描述

公司正在开发一个图形设计软件，其中有一个常用的图形元素是矩形。设计师在工作时可能需要频繁地创建相似的矩形，而这些矩形的基本属性是相同的（颜色、宽度、高度），为了提高设计师的工作效率，请你使用原型模式设计一个矩形对象的原型。使用该原型可以快速克隆生成新的矩形对象。

输入描述

首先输入一个字符串，表示矩形的基本属性信息，包括颜色、长度和宽度，用空格分隔，例如 “Red 10 5”。

然后输入一个整数 N（1 ≤ N ≤ 100），表示使用原型创建的矩形数量。

输出描述

对于每个矩形，输出一行字符串表示矩形的详细信息，如 “Color: Red, Width: 10,Height: 5”。

1
2
3
4
5
6
7
输入
Red 10 5
3
输出
Color: Red, Width: 10, Height: 5
Color: Red, Width: 10, Height: 5
Color: Red, Width: 10, Height: 5

题解

不知道为什么在main方法里get不管用，在Square里面toString就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
import java.util.Scanner;

abstract class Type implements Cloneable {
    public abstract Type clone();
}

class SquareType extends Type {
    private String color;
    private int width;
    private int height;
    
    public SquareType(String color,int width,int height) {
        this.color = color;
        this.width = width;
        this.height = height;
    }
    
    @Override
    public SquareType clone() {
        return new SquareType(this.color,this.width,this.height);
    }
    
    public String getColor(){
        return this.color;
    }
    
    public int getWidth() {
        return this.width;
    }
    
    public int getHeight() {
        return this.height;
    }
    
    @Override
    public String toString() {
        return "Color: " + color + ", Width: " + width + ", Height: " + height;

    }
}

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String color = sc.next();
        int width = sc.nextInt();
        int height = sc.nextInt();
        
        Type originType = new SquareType(color,width,height);
        
        int n = sc.nextInt();
        for (int i = 0;i<n;++i){
            Type clone = originType.clone();
            System.out.println(clone);
        }
    }
}

695.岛屿的最大面积

题目描述

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

1
2
3
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

题解

此题可以利用深度优先搜索进行解答，外层函数遍历所有位置，寻找可以进行搜索的地方，随后将其存入栈中开始搜索，搜索结束记录本次搜索面积，将其与最大面积进行比较，遍历结束后返回最大面积即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
vector<int> direction{-1,0,1,0,-1};
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        //行
        int m = grid.size();
        //列
        int n = m? grid[0].size() : 0;
        int max_area = 0,area,x,y;
        for (int i = 0;i < m;++i){
            for (int j = 0;j < n;++j) {
                if (grid[i][j]){
                    area = 1;
                    //这样就不会重复遍历啦
                    grid[i][j] = 0;
                    stack<pair<int,int>> island;
                    island.push({i,j});
                    while(!island.empty()) {
                        auto [r,c] = island.top();
                        island.pop();
                        //遍历四个方向
                        for (int k = 0;k<4;++k) {
                            x = r + direction[k];
                            y = c + direction[k+1];
                            
                            if (x < 0 || x >= m || y< 0 || y >= n) continue;
                            //相邻有岛屿
                            if (grid[x][y]) {
                                ++area;
                                grid[x][y] = 0;
                                island.push({x,y});
                            }                         
                        }
                    }
                    max_area = max(max_area,area);
                }
            }
        }
        return max_area;
    }
};

栈的优点就是特别好理解，并且不容易出现栈满的情况，也可以使用递归解答本题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
vector<int> direction{-1,0,1,0,-1};
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        //行
        int m = grid.size();
        //列
        int n = m? grid[0].size() : 0;
        int max_area = 0,area,x,y;
        for (int i = 0;i < m;++i){
            for (int j = 0;j < n;++j) {
                if (grid[i][j]){
                    area = dfs(grid,i,j);
                    max_area = max(max_area,area);
                }
            }
        }
        return max_area;
    }
    int dfs(vector<vector<int>> & grid,int i,int j) {
        grid[i][j] = 0;
        int x,y,area = 1;
        int m = grid.size();
        int n = m? grid[0].size() : 0;
        for (int k = 0;k<4;++k) {
            x = i + direction[k];
            y = j + direction[k+1];
            if (x < 0 || x >= m || y < 0 || y >= n) continue;
            if (grid[x][y]) {
                area += dfs(grid,x,y);
            }
        }
        return area;
    }
};

994.腐烂的橘子

题目描述

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

  • 值 0 代表空单元格；
  • 值 1 代表新鲜橘子；
  • 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

1
2
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

题解

家人们谁懂，蛮简单一道题卡在了第一个用例上，排查了半天差点把代码重写，最后发现是因为把 = 写成了 ==

与上一题类似，同样遍历整个数组，寻找烂掉的橘子，并从烂橘子开始，遍历四个相邻方向，若有新鲜橘子，则将其腐烂。不同的是，由于每一轮烂橘子都会腐蚀周围橘子，所以使用广度优先搜索，搜索的深度即为所求分钟数。此处可使用列表进行搜索，并使用一个变量cnt记录剩余新鲜橘子数量。先完全遍历数组，将烂橘子放入队列bad中，得到新鲜橘子cnt个，随后一次从bad中取出橘子，遍历其四周，若存在新鲜橘子则将其加入队列，并将cnt-1。

至于如何记录轮次，这里使用了一个二维数组round，初始遍历时将每个烂橘子的round设为1，在随后的循环中每个新鲜橘子的round是前一个烂橘子的round+1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
vector<int> direction{-1,0,1,0,-1};
int round[10][10];
public:
    int orangesRotting(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = m ? grid[0].size() : 0;
        queue<pair<int,int>> bad;
        int cnt = 0;
        //统计
        for (int i = 0;i < m;++i) {
            for (int j = 0;j < n;++j) {
                if (grid[i][j] == 1) ++cnt;
                else if (grid[i][j] == 2) {
                    bad.emplace(i,j);
                    round[i][j] = 0;
                }
            }
        }
        
        int x,y,ans = 0;
        while (cnt > 0 && !bad.empty()) {
            auto [r,c] = bad.front();
            bad.pop();
            //遍历四个方向
            for (int k = 0;k < 4;++k) {
                x = r + direction[k]; y = c + direction[k+1];                
                if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y]!=1) continue;
                round[x][y] = round[r][c] + 1;
                grid[x][y] = 2;
                --cnt;
                ans = round[x][y];
                bad.emplace(x,y);                               
            }
            
        }
        
        return cnt? -1 : ans;
        
    }
};

24.9

卡码9.奇怪的信

题目描述

有一天, 小明收到一张奇怪的信, 信上要小明计算出给定数各个位上数字为偶数的和。
例如：5548，结果为12，等于 4 + 8 。
小明很苦恼，想请你帮忙解决这个问题。

输入描述

输入数据有多组。每组占一行，只有一个整整数，保证数字在32位整型范围内。

输出描述

对于每组输入数据，输出一行，每组数据下方有一个空行。

题解

很好理解的一道题，但在类型转换上有一些小问题，记录记录，学习学习

本题无非将一行数据作为字符串进行输入，然后再遍历每一位，将偶数位相加，问题是字符转化为int类型并不会一一对应，如若直接int num = s[i]，得到的结果会大很多，起初尝试atoi()函数，但会报错（

后来发现……可以直接用s[i]-'0'，天才的做法，就此解决

下附源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<iostream>
using namespace std;

int main() {
    string s;
    while(cin >> s) {
        int sum = 0;
        for (int i = 0; i < s.size(); i++) {
            int num = s[i] - '0'; 
            if (num % 2 == 1) continue;
            sum += num;
        }
        cout << sum << endl << endl;
    }
    return 0;
}

努力复健努力复健

卡码11.共同祖先

题目描述

小明发现和小宇有共同祖先！现在小明想知道小宇是他的长辈，晚辈，还是兄弟。

输入描述

输入包含多组测试数据。每组首先输入一个整数N（N<=10），接下来N行，每行输入两个整数a和b，表示a的父亲是b（1<=a,b<=20）。小明的编号为1，小宇的编号为2。
输入数据保证每个人只有一个父亲。

输出描述

对于每组输入，如果小宇是小明的晚辈，则输出“You are my younger”，如果小宇是小明的长辈，则输出“You are my elder”，如果是同辈则输出“You are my brother”。

题解

这道题感觉有些困难的原因出在想复杂了，题目给出的所有用例均在抵达共同祖先时便终止，意味着两人的长辈终止于共同的那一位，所以可以先记录这个亲戚谱系，然后从小明和小宇出发，层层深入，看最终两人分别处于这个树的第几层，通过判断层数大小就可以推断出两人的辈分关系。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
#include<vector>

using namespace std;

int main() {
    int n;
    while(cin >> n) {
        vector<int> nums(30,0);
        int a,b;
        for (int i = 0; i < n; i++) {
            cin >> a >> b;
            nums[a] = b;
        }
        //貌似数据的最后一位就是共同祖先
        int deep1 = 0,deep2 = 0;
        int curr1 = 1,curr2 = 2;
        while (nums[curr1] != 0) {
            deep1++;
            curr1 = nums[curr1];
        }
        while (nums[curr2] != 0) {
            deep2++;
            curr2 = nums[curr2];
        }
        if (deep1 > deep2) {
             cout << "You are my elder" <<endl;
        } else if (deep1 < deep2) {
            cout << "You are my younger" << endl;
        } else {
            cout << "You are my brother" << endl;
        }
        
    }
    return 0;
}

但是如果这个谱系图可以无限延伸，并不止于共同祖先呢？

私以为这样会复杂一些

卡码14.句子缩写

题目描述

输出一个词组中每个单词的首字母的大写组合。

输入描述

输入的第一行是一个整数n，表示一共有n组测试数据。（输入只有一个n，没有多组n的输入）
接下来有n行，每组测试数据占一行，每行有一个词组，每个词组由一个或多个单词组成；每组的单词个数不超过10个，每个单词有一个或多个大写或小写字母组成；
单词长度不超过10，由一个或多个空格分隔这些单词。

输出描述

请为每组测试数据输出规定的缩写，每组输出占一行。

题解

这道题不难想，无非获取一整行输入，然后根据空格将句子中的单词切分进string数组，最后遍历数组，将每个单词的首字母转换为大写输出即可；

至于遇到了什么坑呢？

代码运行时，由于测试用例只有一行，打印出的内容为空，但若有多条数据，便总会少一条，怎么回事捏

原因在于输入n后换行，包含一个回车键，若直接getline()读取一整行信息，相当于只读取了回车键，所以需要使用getchar()吸收回车，使得能获取下一行数据

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<iostream>
#include<vector>
#include<sstream>
#include<string>
 
using namespace std;
 
int main() {
    int n;
    cin >> n;
    getchar();  // 坑！！！！回去记录
    for (int i = 0; i < n; i++) {
        string stm;
        getline(cin,stm);
        istringstream iss(stm);
        vector<string> words(10);
        string word;
        while(iss >> word) {
            words.push_back(word);
            if (word[0] >= 'a' && word[0] <= 'z') {
                word[0] -= 32;
            }
            cout << word[0];
        }
        if (i != n-1) {
            cout << endl;
        }
    }
    return 0;
}

卡码17.出栈合法性

题目描述

已知自然数1，2，…，N（1<=N<=100）依次入栈，请问序列C1，C2，…，CN是否为合法的出栈序列。

输入描述

输入包含多组测试数据。
每组测试数据的第一行为整数N（1<=N<=100），当N=0时，输入结束。
第二行为N个正整数，以空格隔开，为出栈序列。

输出描述

对于每组输入，输出结果为一行字符串。
如给出的序列是合法的出栈序列，则输出Yes，否则输出No。

题解

有两种做法，其一是根据栈的特点，对于当前元素 x，若出栈序列合法，需满足 x 之后所有小于 x 的元素为递减的。遍历输出序列，对每个元素进行check，确保其后小于它的所有元素递减。

第二种为模拟栈，若出栈序列合法，则最终栈内元素应为空，由此判断是否合法

先将出栈序列录入数组，然后依次将元素入栈，若栈顶元素与出栈序列当前元素相同，则将其出栈。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<iostream>
#include<vector>
#include<stack>
 
using namespace std;

int main() {
    int n;
    while (cin >> n) {
        if (n == 0) break;
        vector<int> a(n);
        for (int i = 0; i < n; i++) {
            cin >> a[i];
        }
        stack<int> stk;
        int j = 0;
        for (int i = 1; i <= n; i++) {
            stk.push(i);
            while (!stk.empty() && stk.top()==a[j]) {
                stk.pop();
                j++;
            }
        }
        if(stk.empty()) 
            puts("Yes");
        else
            puts("No");
    }
    return 0;
}

卡码18.链表的基本操作

不是很难，但太久没写过链表了，还是有一些小问题，来记录一下

题目描述

本题考察链表的基本操作。温馨提示：本题较为复杂，需要细心多花一些时间。

输入描述

输入数据只有一组，第一行有n+1个整数，第一个整数是这行余下的整数数目n，后面是n个整数。

这一行整数是用来初始化列表的，并且输入的顺序与列表中的顺序相反，也就是说如果列表中是1、2、3那么输入的顺序是3、2、1。

第二行有一个整数m，代表下面还有m行。每行有一个字符串，字符串是“get”，“insert”，“delete”，“show”中的一种。

如果是“get”，代表获得第a个元素。（a从1开始计数）

如果是“delete”，代表删除第a个元素。（a从1开始计数）

如果是“insert”，则其后跟着两个整数a和e，代表在第a个位置前面插入e。（a从1开始计数）

“show”之后没有正数，直接打印链表全部内容。

输出描述

如果获取成功，则输出该元素；

如果删除成功，则输出“delete OK”；

如果获取失败，则输出“get fail”

如果删除失败，则输出“delete fail”

如果插入成功，则输出“insert OK”，否则输出“insert fail”。

如果是“show”，则输出列表中的所有元素，如果列表是空的，则输出“Link list is empty”

注：所有的双引号均不输出。

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include<iostream>

using namespace std;

struct LinkedList {
  int val;
  LinkedList* next;
  LinkedList (int val): val(val), next(nullptr){}
  LinkedList (int val,LinkedList* next): val(val), next(next){}
};

class ListOpr {
public:
    ListOpr() {
        list = new LinkedList(0);
        size = 0;
    }
    void add(int val) {
        LinkedList* node = new LinkedList(val);
        node->next = list->next;
        list->next = node;
        ++size;
    }
    void show() {
        LinkedList* curr = list;
        curr = curr->next;
        if (curr == nullptr) {
            cout << "Link list is empty" << endl;
            return;
        }
        while(curr != nullptr) {
            cout << curr->val << " ";
            curr = curr->next;
        }
        cout << endl;
    }
    void get(int a) {
        LinkedList* curr = list;
        if(size < a || a <= 0) {
            cout << "get fail" << endl;
            return;
        }
        for (int i = 0; i < a; i++) {
            curr = curr->next;
        }
        cout << curr->val << endl;
    }
    void insert(int a,int e) {
        LinkedList* temp;
        LinkedList* head = list;
        if(a <= 0 || (size > 0 && a > size) || (size == 0 && a > 1)) {
            cout << "insert fail" << endl;
            return;
        }
        if(a == 1) {
            add(e);
        } else {
            for (int i = 1; i < a; i++) {
                list = list->next;
            }
            temp = list->next;
            list->next = new LinkedList(e,temp);
            list = head;
        }
        ++size;
        cout << "insert OK" << endl;
    }
    void deleteAtIndex(int a) {
        LinkedList* head = list;
        if(a > size || a <= 0) {
            cout << "delete fail" << endl;
            return;
        }
        if(a == 1) {
            list->next = list->next->next;
        } else {
            for (int i = 0; i < a-1; i++) {
                list = list->next;
            }
            list->next = list->next->next;
            list = head;
        }
        --size;
        cout << "delete OK" << endl;
    }
    

private:
    int size;
    LinkedList* list;
};

int main() {
    int n,value,m;
    cin >> n;
    ListOpr link;
    for (int i = 0; i < n; i++) {
        cin >> value;
        link.add(value);
    }
    cin >> m;
    for (int i = 0; i < m; i++) {
        string opr;
        int a,e;
        cin >> opr;
        if(opr == "get") {
            cin >> a;
            link.get(a);
        } else if (opr == "delete") {
            cin >> a;
            link.deleteAtIndex(a);
        } else if (opr == "insert") {
            cin >> a >> e;
            link.insert(a,e);
        } else if (opr == "show") {
            link.show();
        }
    }
    return 0;
}

卡码20.删除重复元素

题目描述

根据一个递增的整数序列构造有序单链表，删除其中的重复元素

输入描述

输入包括多组测试数据，每组测试数据占一行，第一个为大于等于0的整数n，表示该单链表的长度，后面跟着n个整数，表示链表的每一个元素。整数之间用空格隔开

输出描述

针对每组测试数据，输出包括两行，分别是删除前和删除后的链表元素，用空格隔开

如果链表为空，则只输出一行，list is empty

题解

删除的时候有一个小坑，我这里的处理方法逻辑是，循环链表现有元素，如果重复就将其删掉，是一个双重嵌套循环，删除后将指针往后移一个，如果没有重复就直接往后移，问题就出在这里，没有重复的后移并没有套在else的方法体里面，所以——如果重复就会后移两位，于是若最后一个元素需要删除，就会出现指针越界的情况。

放一下长长的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<iostream>

using namespace std;

struct LinkedList {
    int val;
    LinkedList* next;
    LinkedList(){}
    LinkedList(int val): val(val),next(nullptr){}
};

class ListOpr {
public:
    ListOpr() {
        list = new LinkedList(0);
        tail = list;
        size = 0;
    }
    void add(int val) {
        LinkedList* node = new LinkedList(val);
        tail->next = node;
        tail = tail->next;
        ++size;
    }
    void deleteSame() {
        LinkedList* curr = list;
        curr = curr->next;
        while(curr != nullptr) {
            LinkedList* temp = curr;
            while(temp->next != nullptr) {
                if (curr->val == temp->next->val) {
                    temp->next = temp->next->next;
                    --size;
                } else {
                    //问题就出在这里！！！
                    temp = temp->next;   
                }
            }
            curr = curr->next;
        }
    }
    void show() {
        LinkedList* curr = list;
        if(size == 0) {
            cout << "list is empty" << endl;
            return;
        }
        curr = curr->next;
        while(curr != nullptr) {
            cout << curr->val << " ";
            curr = curr->next;
        }
        cout << endl;
    }
private:
    int size;
    LinkedList* list;
    LinkedList* tail;
};
int main() {
    int n,value;
    while(cin >> n) {
        ListOpr link;
        for (int i = 0; i < n; i++) {
            cin >> value;
            link.add(value);
        }
        link.show();
        if (n == 0) continue;
        link.deleteSame();
        link.show();
    }
    return 0;
}