【2024算法设计与分析】复习提纲与往年题
考试时间;16周周二(6.11)

复习大纲
第1、2、3、4章
算法复杂性,时间复杂性/空间复杂性
函数的增长,渐进符号Θ, O, Ω
分而治之:基本思想,归并排序、最大子数组;以归并排序讲解分治法的基本思想
f(n) = O(g(n) f(n) = Θ(g(n)) f(n)= Ω(g(n))等含义? O(n), Θ(n),Ω(n)的含义?
f(n)= Θ(g(n))等含义? O(n), Θ(n), Ω(n)的含义?
单源最短路径、多源最短路径、 Dijkstra算法、Bellman-Ford算法、归并排序、最小生成树、深度优先搜索、广度优先搜索等算法的时间复杂度。

第15章 动态规划
- 动态规划原理,最优子结构,设计和分析动态规划算法;
- 两个问题,钢条切割、矩阵链乘法,最长公共子序列;



第16章 贪心算法
- 贪心算法原理,设计和分析贪心算法;
- 活动选择问题;0/1背包问题,分数背包问题等;

第24章 单源最短路
最短路的性质和定理
Bellman-Ford算法,Dijkstra算法
第25章 所有顶点对之间的最短路
- 按边数分解的(基于矩阵乘法的)动态规划算法。
- 按顶点编号分解的(Floyd-Warshall)动态规划算法。

第26章 最大流
- 流网络的基本概念和性质
- 最大流问题的增广路算法,最大流最小割定理
- 使用最大流的方法计算最大匹配
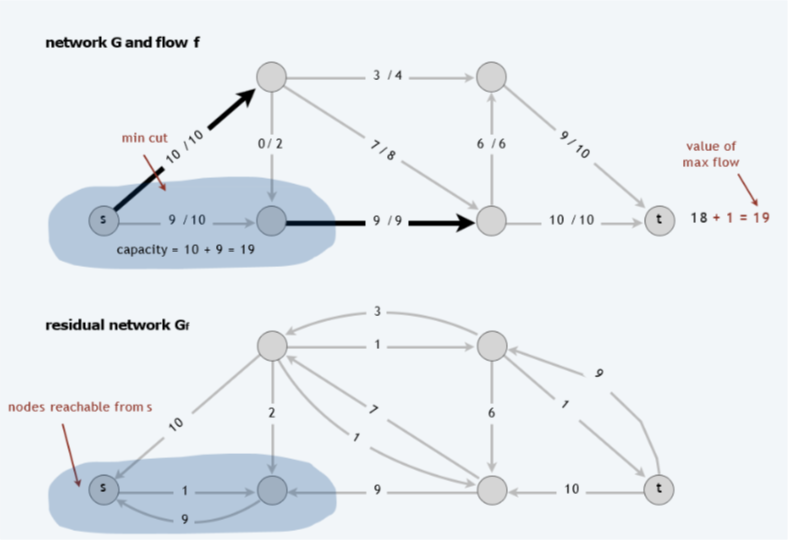
给定一个有向流网络,找出每条增广路径,确定最大流和最小割最大流的流量等于最小割的流量
第34章 NPC
- P、NP、NPC、NP-hard、多项式归约的概念和性质,P=NP和P≠NP的涵义
- 给出复杂性类P、NP、NP-Complete 和 NP-Hard的定义;
- 给出多项式时间归约及其传递性的定义;解释“P=NP?”问题的含义
- NPc的证明
- NP问题是一个非确定性多项式时间可解的判定问题,因此是一个非确定性算法,可分解为猜想和验证,确定的多项式时间可验证,因此是一个指数级时间算法。
- 通过顶点覆盖是NP-hard问题证明团问题也是NP-hard问题
第35章 近似算法
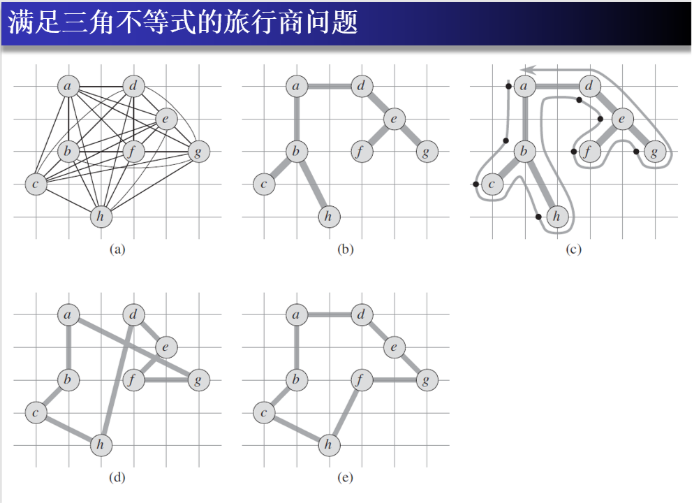
- 满足三角不等式的TSP问题的近似算法
- 顶点覆盖问题的近似算法
往年题
2024年回忆版
一、概念题(英文)
解释大O、大Ω、大Θ、多项式归约、P、NP、NPC
二、(中文)
钢条切割问题。思想,伪代码,时间复杂度
三、(中文)
定义子图同构问题:
Input:无向简单图G(V,E),H(V1,E1)
Output:G中存在子图与H同构则输出真、否则输出假
请借助团问题,证明子图同构问题是NPC问题
四、(英文)
给定一个整数序列。
定义序列中的 “ inversion ” 如下:
一个元素,它和位于其后位置的比它小的元素构成一个inversion
例如74386,inversion为74,73,76,43,86,其总数为5,求一个任意序列的inversion总数。
类比归并排序算法,给出算法思路,伪代码,时间复杂度
五、(中文)
数组A[1]-A[n],表示有n个团队,第i个团队有A[i]人。
数组B[1]-B[m],表示有m个会议室,第j个会议室能容纳B[i]人。
每个团队需要一个会议室开会,他们只会进入会议室容量不小于团队人数的会议室。
现在n个团队同时使用会议室,请设计一个贪心算法,为团队分配会议室,使得能够同时开会的团队数最多。
写出算法思想,伪代码,时间复杂度,正确性证明。
六、(中文)
叙述多源最短路径的矩阵乘法算法的思想。
给出一个有向图,给出有向图的邻接矩阵L1,补全L2和L3。
写出从结点b到其他结点的最短路径
七、(英文)
给出顶点覆盖问题的一种近似算法,给出算法思路、伪代码、求出其近似比(证明是2近似算法)。
2020年回忆版
一(30分)
某个点的最短边是否属于某课最小生成树,如果是,请证明。
要求你给出一个求强连通分量的算法,并且证明正确性
网络流的一个割,其中一条边去掉之后,最大流是多少
二(20分)
给出3SAT问题和Independent Set问题的判定形式,并证明:Independent Set问题是NP-hard问题
网络流算法中,找到增广路径后,证明新的流是合法的(流量守恒and容量限制)
三(15分)
求单源最长路径,要求使用动态规划算法(bellman-ford算法即可)
伪代码,时间复杂度,思想,动态规划方程
四(15分)
描述Floyd算法思想,给矩阵D0D2 求D1D3(理解Floyd算法就会做)
五(20分)
动态规划算法设计:
n个题目,每个题目有mi的做题时间和vi的分数
问得到V分数的前提下,最少需要多少时间做题(假设题目全对)
写动规方程,算法思路,伪代码,设计一个时间复杂度为mV的算法
1 | 应该是能设计出一个时间复杂度为nV的算法,而非mV |
2021年回忆版
- 辨析O,Θ,Ω三个渐进符号的相同点和不同点
- 主定理的应用(第三种情况)
- 证明顶点覆盖问题是NPC问题
- 强连通分量算法,时间复杂度,正确性证明
- Floyd-Warshall算法思想
- 有关图的一道证明题
- 证明最短路径的子路径也是最短路径
- 证明所有最短路径不含圈
- 证明u到v的最短路径<=u到s的最短路径+w(s,v)
- 一道算法设计题:
一个图的权值由w增大为w’,设计算法更新他的最小生成树
输入一个图G,他的最小生成树 T,一条边e,新权值w - 一道动态规划题,大概意思是,有n堆沙子,每堆沙子有自己的重量
每次只能合并相邻的两堆沙子,合并所需要的力气为两堆沙子重量之和,设计算法求合并n堆沙子的最小力气。 - 贪心
和活动选择问题基本一样,要复习活动选择问题的伪代码和正确性证明。
2019年回忆版
说明算法的时间复杂度为O(n2)与问题的时间复杂度为O(n2)含义与区别
简述贪婪算法的基本思想·
对于一个有向无圈图DAG,其中顶点s入度为0,t出度为0,设计算法求s到t的最长路径的长度,简述算法的基本思想,写出伪代码并分析其时间复杂度
证明
- 安全边定理
- 最大流最小割定理
- 求单源点最短路径中,设源点s到顶点v的最短路径包含的边数为k,证明在Bellmanford算法中,经过第k次循环后,得到s到顶点v的最短距离
写出Ford-Fulkerson算法的伪代码,假设流网络中容量均为整数,且最大流量为C,试分析算法的时间复杂度,求出如下流网络中最大流和最小割
写出求有向图的强连通分支的伪代码,并给出证明
简述Floyd-Warshall算法的基本思想,对如下有向图,已知D(0)矩阵如下图所示,求出其D(1),D(2),D(3)矩阵
2022年回忆版
一、选择题(2分一个)
- $f(n)=\frac{1}{100}n^3+20n+3$判断$f(n)= O(n^3)$还是$f(n)=\Theta(n^3)$还是都是都不是
- DFS过程中不会出现什么边(选项是前向边后向边交叉边排列组合)
- $G$ 和 $G^T$的强连通分支是否相同(显然相同)
- 考了一个三角不等式 $δ(s,v)≤δ(s,u)+w(u,v)$
- Bellman-Ford算法的时间复杂度(O(VE))
二、填空题(3分一个)
RAM包含哪三个基本指令(算术指令,数据移动指令,控制指令)
在BFS过程中,对边(u,v)考察了$\delta(s,u)$和$\delta(s,v)$的关系
$\delta(s,v) \leq \delta(s,u)+1$
- DFS的时间复杂度 $(O(V+E))$
松弛后的状态(就考了松弛定理,$v.d=δ(s,v)$)
$l_{ij}^{(m)}=min{ {l_{ik}^{(m-1)}+w_{kj}} }$ 中m的含义
三、解答题
(10分)$T(n)=2T(n/5)+n^2lgn$,求 upper asymptotic bound。(英文题)
(10分)给出多项式归约和传递性的定义,解释$N=NP$问题的意义。
(15分)
a. 写出求MST的伪代码和时间复杂度
b. 如果在图G = ( V , E ) 顶点不变的基础之上,已知有一颗最小生成树T,那么加入边( u , v ),u , v ∈ G . V 。请设计有效的算法判断加入边之后原来的最小生成树T是否仍旧是现在的新图的最小生成树,写出伪代码、算法正确性证明和复杂度。(英文题)
(15分)Floyd-Warshall算法,写出算法思想,补全矩阵$D_{[4]}$,写出所有多源最短路径,并给出复杂度。(英文题)
(25分)算法设计题
- 用动态规划求出由a,b,c组成的n位不含连续两个a都字符串数目,写出算法思想、伪代码、时间空间复杂度;(15分)
- 集合覆盖问题,要求用贪心算法实现从F中找最少数目的集合,求算法思想、伪代码并验证算法正确性.(10分)
评价:尽管增加了25的客观题(几乎送分),这次算法考试难度还是很大,我们又是第一次改成必修课(在之前都是选修),所以算法成绩出来几乎是一片哀嚎。全年级卷面分上90的就没两个,平时分30%的情况下最终上90的也只有5个人,最高分应该是5班的同学95分。主要难点在于算法设计题,相较于往年,显得十分反套路和复杂。
23年回忆版
一、概念题
1.O(n²)和Ω(n²)的含义
2.以归并排序为例子阐述分治算法的思想
二、算法题
区间覆盖问题,并证明贪心正确性
a1,a2……an中相邻的两个数只能选择其中一个,怎么选能够得到最大和。使用动态规划算法。
(1)写出目标函数
(2)根据目标函数写出递推方程
(3)根据递推方程求出时间复杂度
Floyd-Warshall算法
(1)写出目标函数和递推方程
(2)根据下图补全Floyd-Warshall算法的过程
Ford-Fulkson算法过程,写出最大流和最小割
三、证明题
- 证明最大流最小割定理
- 顶点覆盖和团问题相关
- 证明TSP的近似算法是2-近似算法



